Simultaneous block diagonalization

Synopsis

Many biological and technological networks show intricate synchronization patterns, where several internally coherent but mutually independent clusters coexist. Maintaining the desired dynamical patterns is critical to the function of those networked systems. For instance, long-range synchronization in the theta frequency band between the prefrontal cortex and the temporal cortex has been shown to improve working memory in older adults.

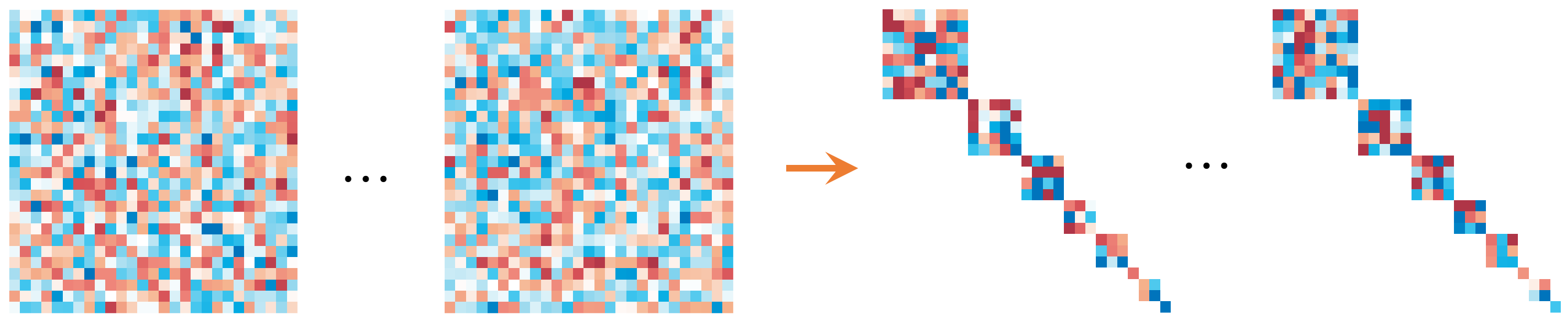
Analyzing cluster synchronization patterns: Is symmetry really your friend? Which synchronization patterns we can ultimately observe are determined by their stabilities. It is widely believed that utilizing symmetries in the network structure is crucial to the characterization of a pattern’s stability. However, symmetry-based methods are limited in the types of synchronization patterns they can directly treat and can be computationally expensive. So far, the search for a fast and versatile method to analyze synchronization patterns has remained elusive. Interestingly, we found that when symmetry information is discarded, the problem becomes easier, not harder. By forgoing symmetry, we not only can treat all synchronization patterns in a unified fashion but also develop algorithms that are orders of magnitude faster than symmetry-based ones [SIAM Rev. 62, 817–836 (2020)]. Our symmetry-independent method is based on finding the finest simultaneous block diagonalization (SBD) of noncommuting matrices in the variational equation and can potentially be applied to other problems where multiple matrices need to be simplified concurrently.

Unifying the treatment of higher-order, multilayer, and temporal interactions. Over the past two decades, networks have emerged as a versatile description of interconnected complex systems. However, it has also become increasingly clear that the original formulation of a static network representing a single type of pairwise interaction has its limitations. For this reason, the original formulation has been generalized in different directions, including hypergraphs that account for nonpairwise interactions, multilayer networks that accommodate mixed types of interactions, and temporal networks for interaction patterns that change over time. Naturally, with the increased descriptive power comes an increased analytical complexity, especially for dynamical processes on these generalized networks. The same SBD framework can be extended to optimally reduce the analytical complexity in all three classes of generalized networks and can thus facilitate the discovery of novel emergent phenomena in complex systems with generalized interactions [Commun. Phys. 4, 195 (2021)].

Code

Our code for finding a simultaneous block diagonalization of an arbitrary number of matrices can be found here and here.

Press

• New tool untangles complex dynamics on hypergraphs—SFI News

References

• Y. Zhang and A. E. Motter, Symmetry-independent stability analysis of synchronization patterns, SIAM Rev. 62, 817–836 (2020)
• Y. Zhang, V. Latora, and A. E. Motter, Unified treatment of synchronization patterns in generalized networks with higher-order, multilayer, and temporal interactions, Commun. Phys. 4, 195 (2021)
• F. M. Brady*, Y. Zhang*, and A. E. Motter, Forget partitions: Cluster synchronization in directed networks generate hierarchies, arXiv:2106.13220