Temporal sync
Synopsis
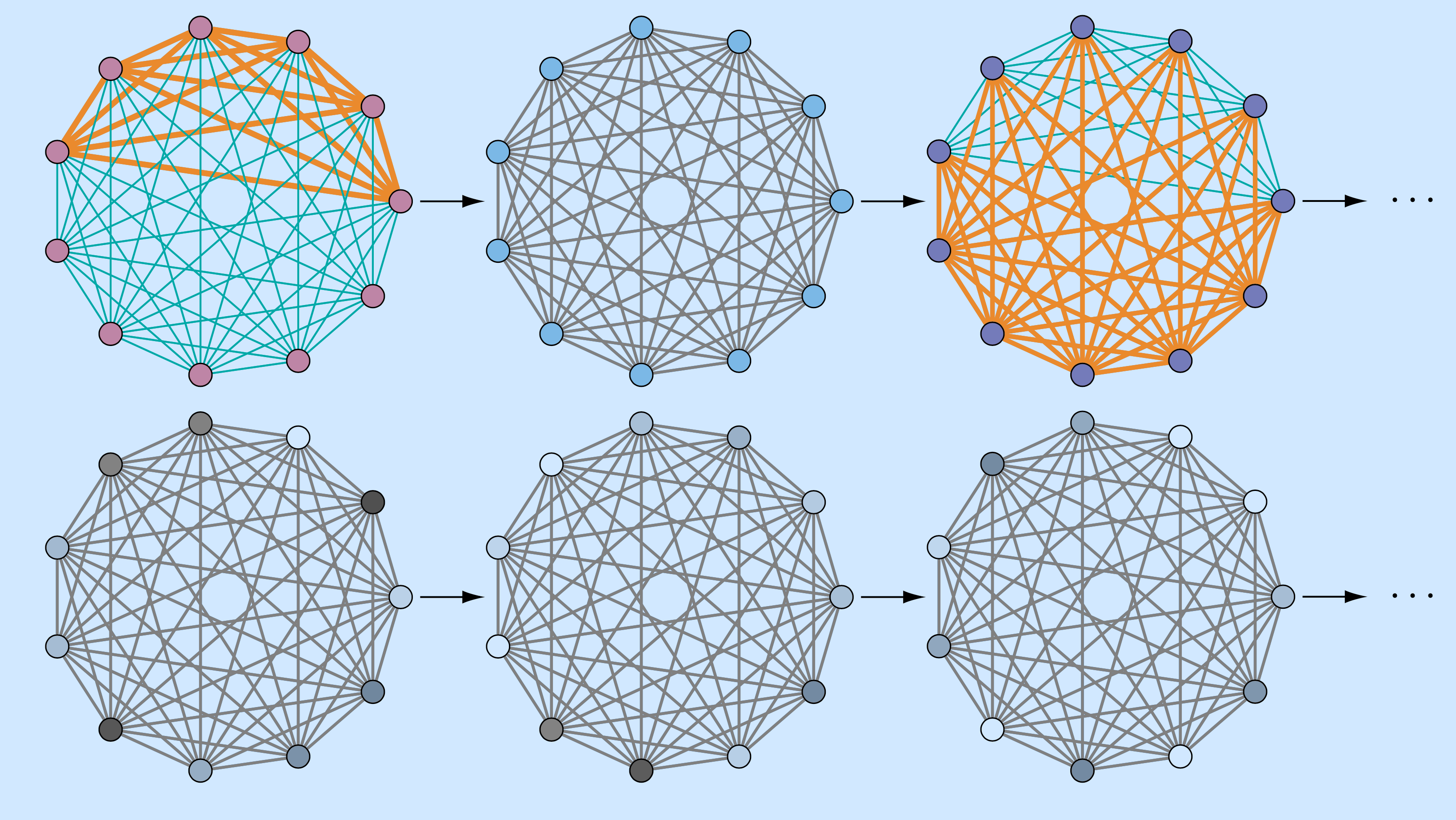
From power grids to neuronal populations, getting in sync is critical to the function of many distributed systems. Being fundamentally a non-equilibrium process, synchronization costs energy and resources to maintain. It is thus important to find strategies that can synchronize a system at the lowest cost in resources. One such resource is the coupling budget available in a network to facilitate the interaction and communication between individual neurons or power generators. For time-independent interactions (often represented by static networks), there is a well-defined lower bound on the amount of coupling that is required for a system to synchronize stably. However, when the network itself is allowed to be dynamic, much less is known.
Our new results show that, by allowing the connection patterns to change over time (modeled as temporal networks), one can go below the fundamental limit set by the optimal static networks and synchronize a system more efficiently. Importantly, our design of these temporal networks is open loop, meaning that the same design works out-of-the-box for very different systems. For example, the same temporal network is expected to facilitate synchronization in both power grids and neuronal populations. This versatility makes our design a powerful tool that can be applied to systems that need to synchronize under tight resource constraints.
Press
Talk
Here is me presenting the work at the Systems Neuroscience and Complexity Seminar @ University of Sydney.
Code
The code accompanying this work can be found here.
References
- Y. Zhang and S. H. Strogatz, Designing temporal networks that synchronize under resource constraints, Nat. Commun. 12, 3273 (2021)